Question:
Give step-by-step solution with explanation and final answer: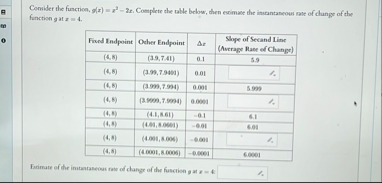
This is AI generated Response.
Asked by: 143
Created at: 2025-05-25 06:53:20
Asked by: 143
Created at: 2025-05-25 06:53:20
Answer:
Rendered
Raw Text
Let's go through the table step by step and fill in the missing values.
**Given function:**
\( g(x) = x^2 - 2x \)
**We want:** The instantaneous rate of change at \( x = 4 \), i.e., \( g'(4) \).
---
### Step 1: Calculate \( g(4) \)
\[
g(4) = (4)^2 - 2 \times 4 = 16 - 8 = 8
\]
---
### Step 2: Fill in the missing \( y \)-values for "Other Endpoint"
- When \( x = 3.9 \):
\[
g(3.9) = (3.9)^2 - 2 \times 3.9 = 15.21 - 7.8 = 7.41
\]
- When \( x = 3.99 \):
\[
g(3.99) = (3.99)^2 - 2 \times 3.99 = 15.9201 - 7.98 = 7.9401
\]
- When \( x = 3.999 \):
\[
g(3.999) = (3.999)^2 - 2 \times 3.999 = 15.992001 - 7.998 = 7.994001
\]
- When \( x = 4.01 \):
\[
g(4.01) = (4.01)^2 - 2 \times 4.01 = 16.0801 - 8.02 = 8.0601
\]
- When \( x = 4.001 \):
\[
g(4.001) = (4.001)^2 - 2 \times 4.001 = 16.008001 - 8.002 = 8.006001
\]
---
### Step 3: Calculate the Slope of the Secant Line
The slope formula:
\[
\text{Slope} = \frac{g(x) - g(4)}{x - 4}
\]
#### For \( x = 3.9 \):
\[
\frac{g(3.9) - g(4)}{3.9 - 4} = \frac{7.41 - 8}{3.9 - 4} = \frac{-0.59}{-0.1} = 5.9
\]
#### For \( x = 3.99 \):
\[
\frac{g(3.99) - g(4)}{3.99 - 4} = \frac{7.9401 - 8}{3.99 - 4} = \frac{-0.0599}{-0.01} = 5.99
\]
#### For \( x = 3.999 \):
\[
\frac{g(3.999) - g(4)}{3.999 - 4} = \frac{7.994001 - 8}{3.999 - 4} = \frac{-0.005999}{-0.001} = 5.999
\]
#### For \( x = 4.01 \):
\[
\frac{g(4.01) - g(4)}{4.01 - 4} = \frac{8.0601 - 8}{0.01} = \frac{0.0601}{0.01} = 6.01
\]
#### For \( x = 4.001 \):
\[
\frac{g(4.001) - g(4)}{4.001 - 4} = \frac{8.006001 - 8}{0.001} = \frac{0.006001}{0.001} = 6.001
\]
---
### Step 4: Estimate the Instantaneous Rate of Change
As \( \Delta x \to 0 \), the average rate of change approaches **6**.
---
### **Final Answer**
\[
\boxed{6}
\]
So, the estimated instantaneous rate of change of the function \( g(x) \) at \( x = 4 \) is **6**.
---
**Table (Filled):**
| Fixed Endpoint | Other Endpoint | Δx | Slope of Secant Line |
|----------------|------------------------|---------|----------------------|
| (4, 8) | (3.9, 7.41) | -0.1 | 5.9 |
| (4, 8) | (3.99, 7.9401) | -0.01 | 5.99 |
| (4, 8) | (3.999, 7.994001) | -0.001 | 5.999 |
| (4, 8) | (4.01, 8.0601) | 0.01 | 6.01 |
| (4, 8) | (4.001, 8.006001) | 0.001 | 6.001 |
**Estimate of the instantaneous rate of change at \( x = 4 \):**
\[
\boxed{6}
\]
📢 Instructions:
- Ask anything relatd to above question only.
- For new Question goto :